Summary

• Task Arithmetic의 핵심 특성 → 각 태스크가 서로 교차하지 않는 영역에서만 작용
  • 초기 가설 → 작은 변화 영역에서 Neural Tangent Kernel(NTK)을 사용한 predictor처럼 선형적 동작 예상
    • 사전 학습(pretrain)은 가중치 크게 변화 → 비선형적
    • 파인튜닝은 선형적일 것으로 예상
• 실험 결과 → 파인튜닝도 비선형적으로 작동
  • 기존 선형성 가설로는 설명 불가 → Task Arithmetic 작동 메커니즘 재탐색 필요
  • 발견된 핵심 메커니즘 → Weight Disentanglement
• Weight Disentanglement의 의미 → 가중치 공간에서 각 태스크 방향이 서로 다른 입력 공간의 국소화된 영역을 독립적으로 제어
  • 추가 발견 → 이러한 특성은 사전 학습 과정에서 자연스럽게 발현 됨
  • 중요한 검증 → 무작위 초기화 모델에서는 해당 특성 미발견

Motivation

• Pre-Trained Model은 현대 머신러닝 시스템에서 핵심적인 역할 수행
• 다운스트림 태스크 성능 향상, 사람 선호도 반영, 견고성 증가를 위한 모델 편집 필요성 증가
• 기존 모델 편집 방법은 비용이 많이 드는 Joint Fine-Tuning과 인간 피드백에 의존해 확장성 제한

Task Arithmetic과 핵심 특성

• Task Arithmetic과 Weight Interpolation이 비용 효율적이고 확장 가능한 모델 편집 방법으로 등장
  • Task Vector ${\tau }_t$: 파인튜닝된 가중치와 사전 학습된 가중치의 차이 (${\tau }_t={\theta }_t^{\ast }-{\theta }_0$)
  • 서로 다른 태스크에 대한 Task Vector를 더하거나 빼서 모델 성능 조작 가능
• Task Arithmetic은 각 태스크가 서로 교차하지 않는 영역에서만 작용해야 효과적으로 동작
  • 이런 특성은 Property 1(Task Arithmetic)으로 공식화
  • 한 태스크 벡터를 더하는 것이 다른 태스크 영역의 모델 출력을 수정하지 않아야 함

기존 가설: Linear Regime

• Task Arithmetic이 작동하는 이유에 대한 기존 가설
  • 기존 가설: 사전 학습된 모델이 파인튜닝 시 선형 레짐(linear regime)에서 작동
  • Neural Tangent Kernel(NTK)에 의해 동작이 결정된다고 추측
    • 이론적으로 너비가 무한한 신경망에서는 NTK가 일정하게 유지되며 비선형성이 선형화됨
    • 선형 레짐에서는 가중치 공간의 연산이 함수 공간에서 유사하게 유지됨 → ${\theta }_3=\alpha {\theta }_1+\beta {\theta }_2$일 때, $f(x;{\theta }_3)\approx \alpha f(x;{\theta }_1)+\beta f(x;{\theta }_2)$가 유지됨
  • 사전 학습(pretrain)은 큰 파라미터 변화로 이루어지므로 비선형 레짐에서 작동
  • 파인튜닝은 상대적으로 작은 변화로 이루어지므로 선형 레짐에서 작동할 것으로 예상
• 그러나 실험 결과 CLIP 모델은 파인튜닝 시에도 비선형 레짐에서 작동함을 발견
  • 
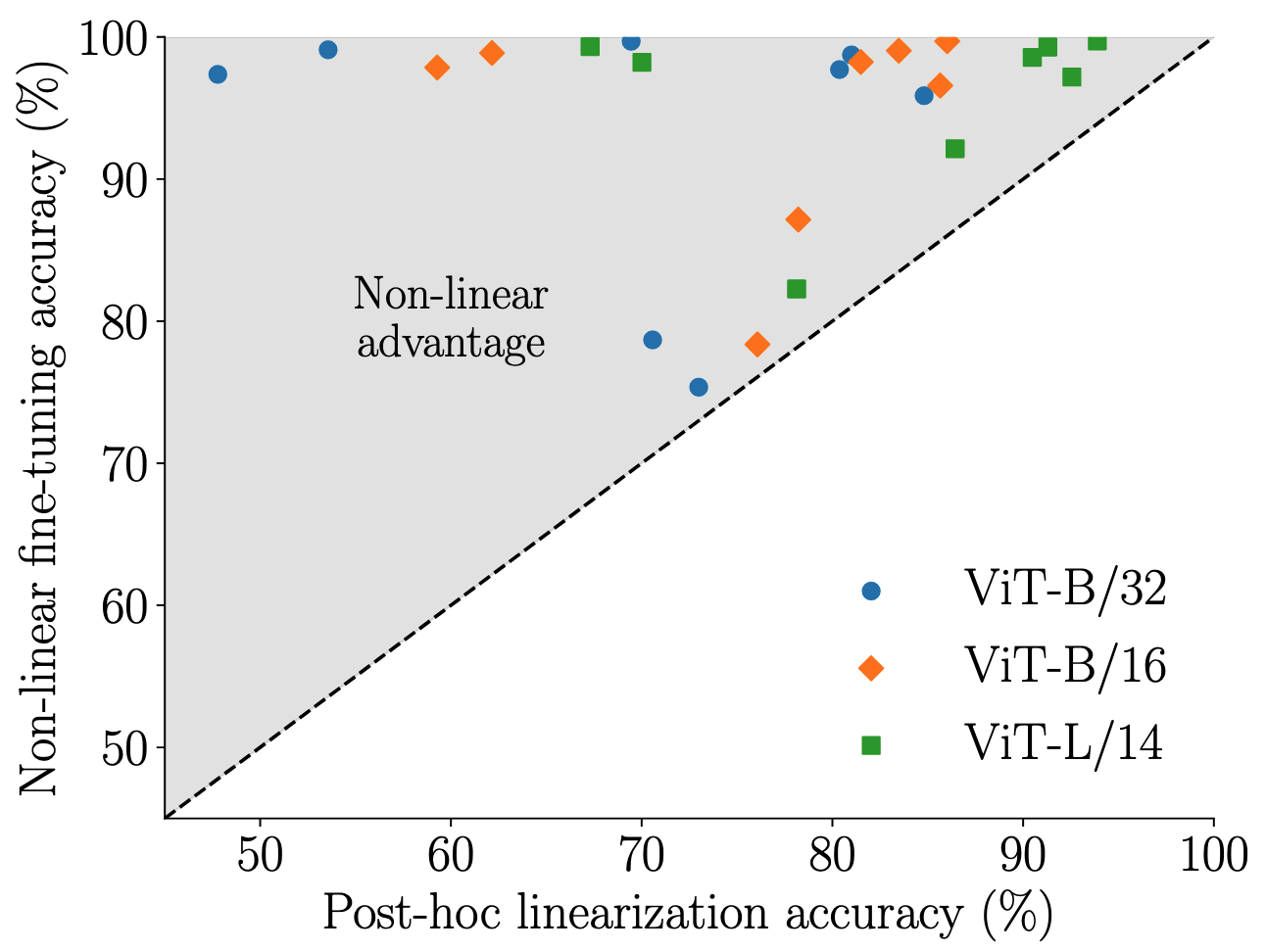
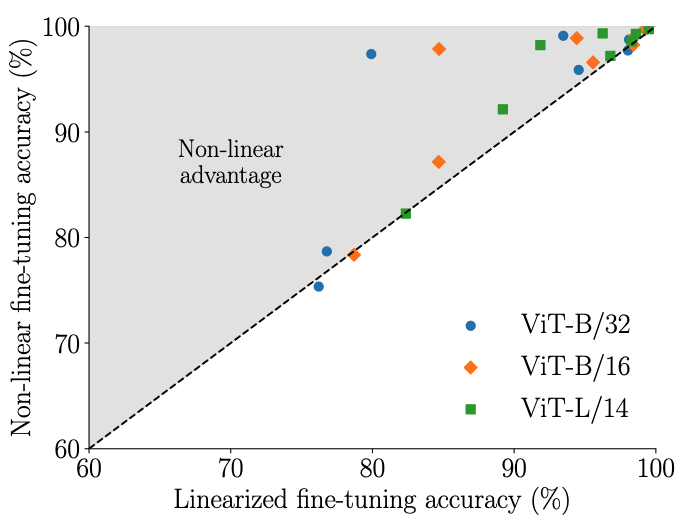
    • NTK가 정상적으로 작동 한다면 (선형 레짐에서 동작 한다면) 비선형 파인 튜닝과 사후 선형화 모델 간 성능 차이가 없어야 함
    • 비선형적으로 파인튜닝된 모델과 사후 선형화 모델 간 큰 성능 차이 존재 → Linear Regime 때문이면 Non-linear advantage가 없어야 함
    • 이는 단순한 선형성만으로 Task Arithmetic을 설명할 수 없음을 시사

Neural Tangent Kernel (NTK)

• Neural Tangent Kernel은 가중치 공간과 함수 공간 사이의 선형 관계를 정의하는 핵심 개념
• 초기화 가중치 ${\theta }_0$ 주변에서 신경망은 1차 테일러 전개로 근사 가능:

• 이 근사는 커널 머신의 예측과 동등해짐: 두 입력 $x$와 $x^{\prime }$ 사이의 NTK는 다음과 같이 정의:

• 선형화된 모델을 훈련한 후 새로운 입력 $x$에 대한 예측은 다음과 같이 표현 가능:

• 여기서 ${\alpha }_i$는 각 훈련 샘플의 가중치, $x_i$는 훈련 데이터 포인트
• 최적 파라미터 ${\theta }^{\ast }={\theta }_0+\sum _{i=1}^n{\alpha }_i{\mathrm{\nabla }}_{\theta }f(x_i;{\theta }_0)$

실제 원인: Weight Disentanglement

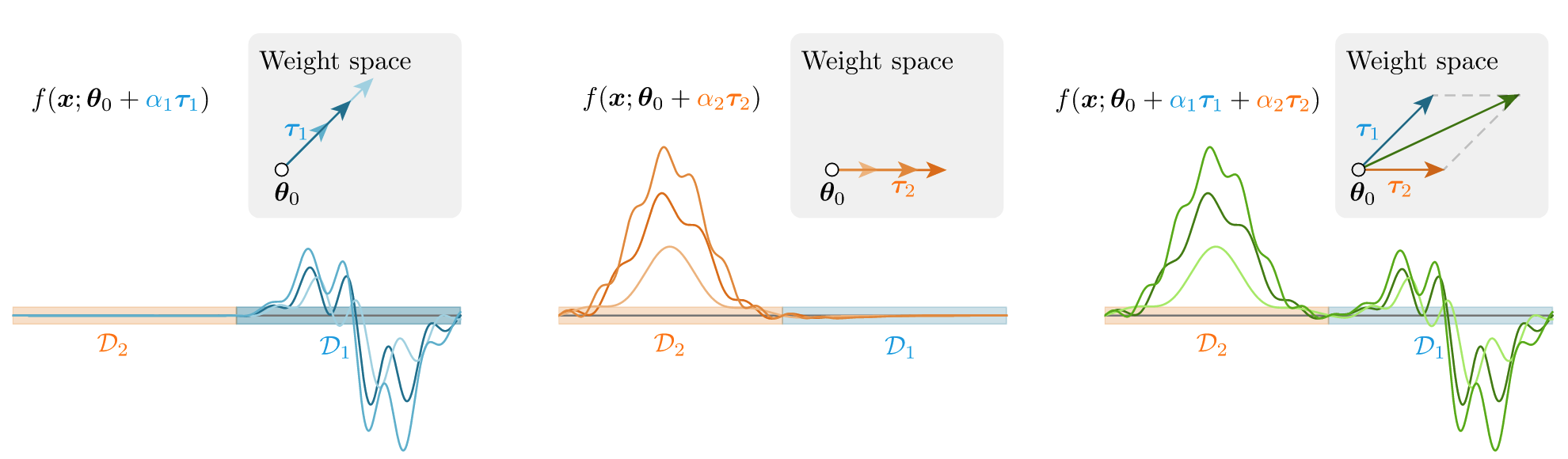
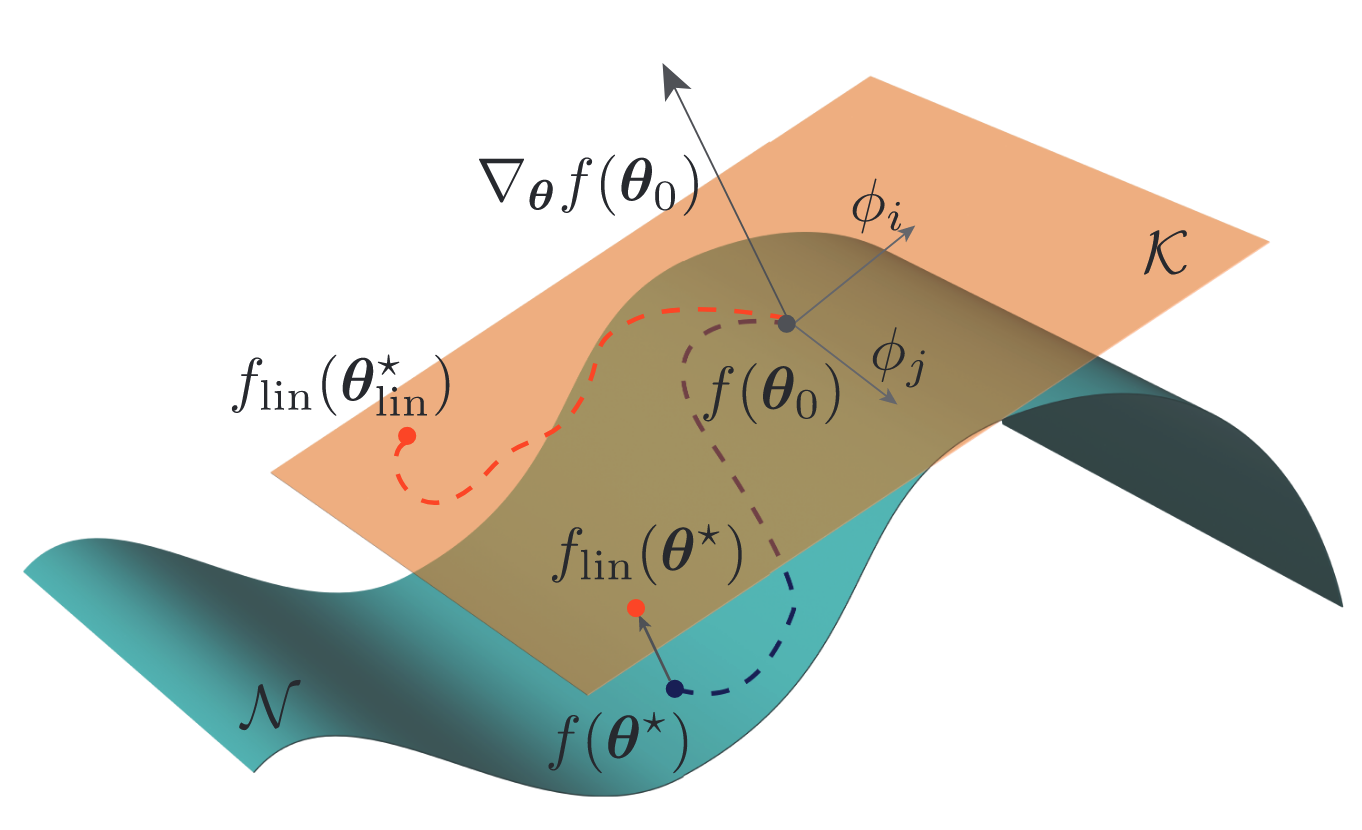
Weight Disentanglement에 대한 시각적 설명

• Weight Disentanglement: 모델의 가중치를 여러 독립적인 컴포넌트로 분해:

1. $g_t(x;{\alpha }_t{\tau }_t)=f(x;{\theta }_0+{\alpha }_t{\tau }_t)=0$ for $x\notin D_t$ and $t=1,\dots ,T$
2. $g_0(x)=0$ for $x\in \bigcup _{t\in [T]}{D}_t$

• Weight Disentanglement가 Task Arithmetic의 실제 필요 조건임을 규명
  • Weight Disentanglement: 가중치 공간의 서로 다른 방향이 입력 공간의 분리된 국소 영역에 대응하는 특성
  • 이를 통해 모델은 독립적으로 가중치 방향 조작 가능
  • 
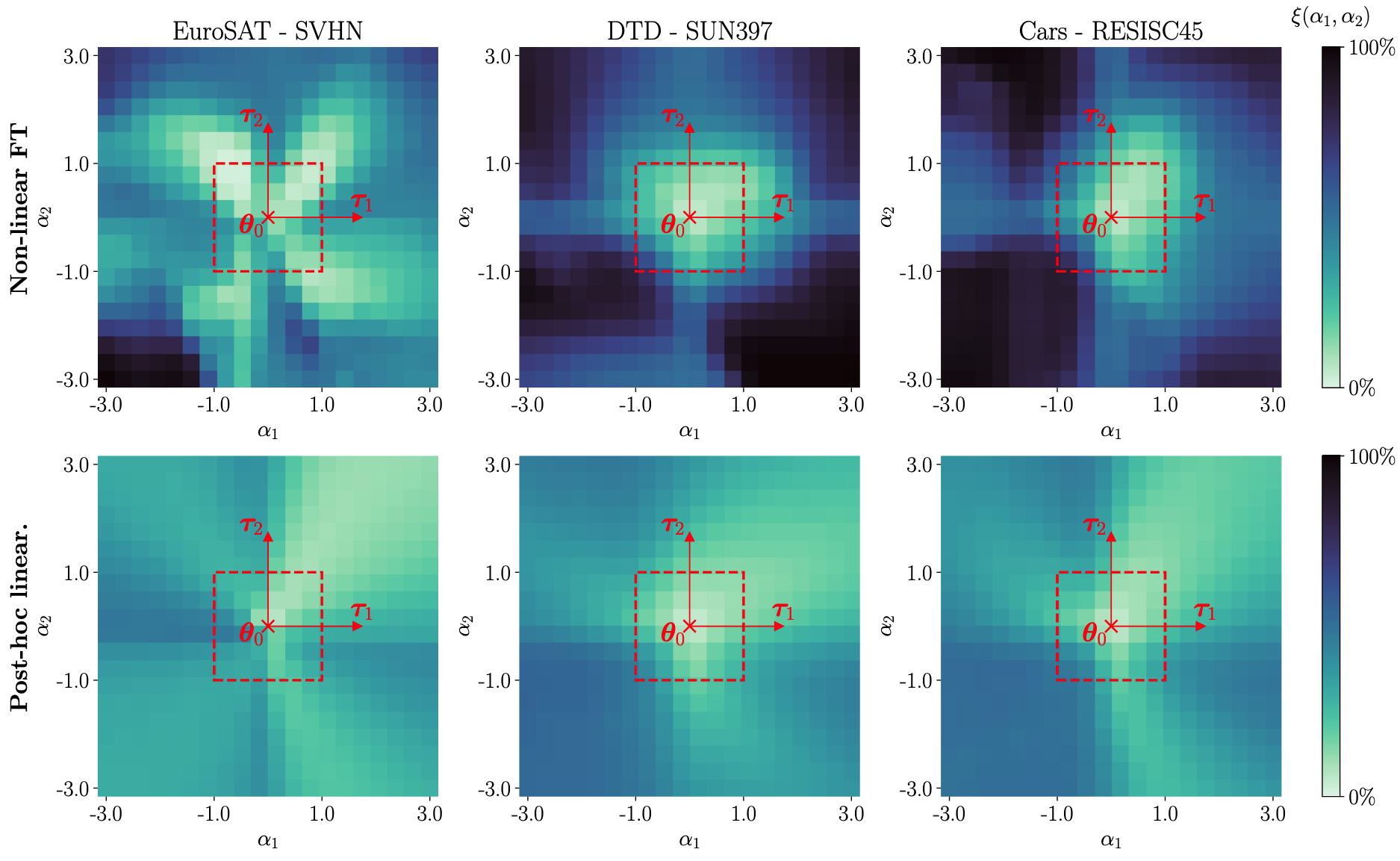
    • 비선형 모델은 ${\theta }_0$ 주변의 작은 영역에서만 낮은 Disentanglement Error 보임
    • 선형화된 모델은 더 넓은 영역에서 낮은 Disentanglement Error 보임
      • 이 때문에 여러 Task Vector를 한 번에 더했을 때의 성능은 선형화된 모델델 더 좋았음
    • NTK 선형화가 Weight Disentanglement를 강화한다는 핵심 통찰

이론적 설명

• NTK Eigenfunction 국소화와 Task Arithmetic의 연관성
  • NTK는 여러 고유함수와 고유값으로 분해 가능: $k_{NTK}(x,x^{\prime })=\sum _{\rho }{\lambda }_{\rho }{\varphi }_{\rho }(x){\varphi }_{\rho }(x^{\prime })$
  • 국소화된 고유함수: 특정 태스크 영역에서만 값을 가지고 다른 영역에서는 거의 0
    • 고유함수가 모든 도메인에서 선형 독립일 경우, 서로 상쇄될 수 없음 → 국소화가 없으면 한 태스크의 고유함수가 다른 태스크 영역에 영향을 미쳐 Task Arithmetic이 불가능 → 즉 이 경우만 아니면 꼭 국소화가 필요한 것은 아님
• 사전 학습이 의미적으로 관련된 특성들을 구조화하는 과정에서 Eigenfunction 국소화가 발생
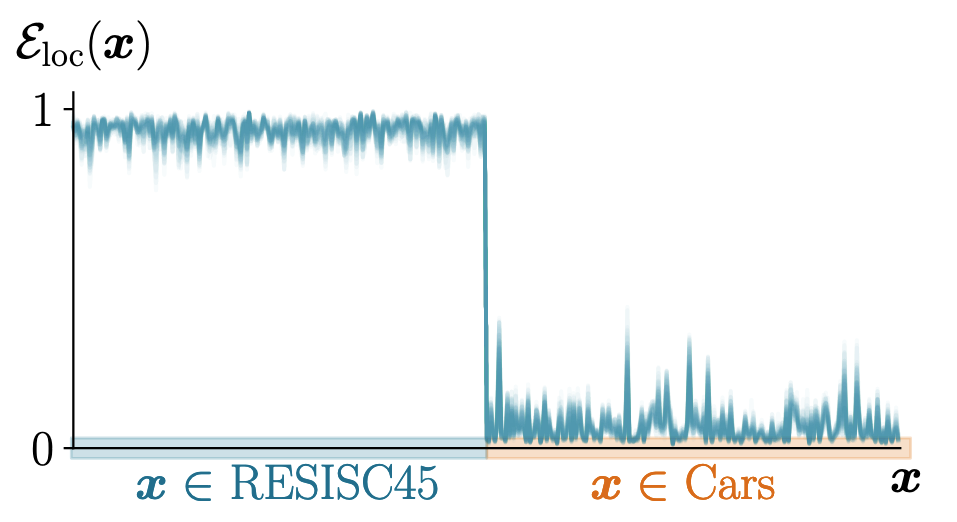
  • → 실제로 RESISC45로 학습된 모델에 대해 해당 데이터와 Cars 데이터의 샘플 $x$에 대해 커널의 Eigenfunctions들의 제곱합을 보면 다른 태스크의 영역에서는 값이 낮음
• Weight Disentanglement는 사전 학습의 창발적 특성임을 발견

Method

$f({\theta }^{\ast })$: Non-Linear FT, $f_{\text{lin}}({\theta }^{\ast })$: Post-Hoc, $f_{\text{lin}}({\theta }_{\text{lin}}^{\ast })$: Linearized FT

1. 비선형 파인튜닝(Non-Linear FT):
   • 사전 학습된 모델 파라미터 ${\theta }_0$에서 시작하여 직접 파인튜닝
   • 결과 모델: $f(x;{\theta }_0+\tau )$, 여기서 $\tau ={\theta }^{\ast }-{\theta }_0$
   • 모델 편집: $f(x;{\theta }_0+\sum _t{\alpha }_t{\tau }_t)$
   • 비선형 레짐에서 작동하여 Weight Disentanglement가 제한적
2. 사후 선형화(Post-Hoc Linearization):
   • 비선형 파인튜닝된 모델을 선형 근사
   • 결과 모델: $f_{lin}(x;{\theta }_0+\tau )=f(x;{\theta }_0)+{\tau }^T{\mathrm{\nabla }}_{\theta }f(x;{\theta }_0)$
   • 모델 편집: $f_{lin}(x;{\theta }_0+\sum _t{\alpha }_t{\tau }_t)=f(x;{\theta }_0)+(\sum _t{\alpha }_t{\tau }_t{)}^T{\mathrm{\nabla }}_{\theta }f(x;{\theta }_0)$
   • 단일 태스크 성능은 저하되지만 Weight Disentanglement는 향상
3. 선형화된 파인튜닝(Linearized FT):
   • 원본 모델 파라미터 ${\theta }_0$를 고정하고 선형화된 모델을 직접 파인튜닝
   • 결과 모델: $f_{lin}(x;{\theta }_0+{\tau }_{lin})=f(x;{\theta }_0)+{\tau }_{lin}^T{\mathrm{\nabla }}_{\theta }f(x;{\theta }_0)$
   • 모델 편집: $f_{lin}(x;{\theta }_0+\sum _t{\alpha }_t{\tau }_{lin,t})=f(x;{\theta }_0)+(\sum _t{\alpha }_t{\tau }_{lin,t}{)}^T{\mathrm{\nabla }}_{\theta }f(x;{\theta }_0)$
   • 원본 모델 파라미터 동결(freeze)하고 차이값 ${\tau }_{lin}$만 학습
   • 실제 구현 방법
     • 원본 모델 파라미터 ${\theta }_0$ 고정(freeze)
     • 새로운 파라미터 ${\tau }_{lin}$을 도입하여 이를 학습
     • 각 순전파 과정에서 초기 출력 $f(x;{\theta }_0)$에 그래디언트-벡터 곱 ${\tau }_{lin}^T{\mathrm{\nabla }}_{\theta }f(x;{\theta }_0)$을 더하여 계산
     • Jacobian-vector product 구현을 통해 계산 효율성 확보

Method 검증

• Non-linear advantage가 Linearized FT를 적용하면 줄어 듦을 발견
  • 
  • ${\tau }_{\text{lin}}$을 이용한 경우 NTK의 근사가 제대로 동작 (근사와 실제 값이 비슷함) → 선형 레짐에서 동작
• 태스크 추가(Task Addition) 실험 결과
  • 선형화 파인튜닝이 비선형 파인튜닝 대비 단일 태스크와 모든 태스크 벡터를 더했을 때의 평균 성능에 대해 우수함
  • 이는 Motivation에서 논의한 Weight Disentanglement 강화로 인한 것으로, Tangent Space에서 파인튜닝이 Task Arithmetic에 효과적임을 입증
  • 정규화된 정확도에서도 선형화 파인튜닝 모델이 더 높은 성능 달성(85.4%, 86.0%, 93.5%)
• 태스크 부정(Task Negation) 실험 결과
  • 선형화 파인튜닝이 제어 태스크 성능을 유지하면서 타겟 태스크 정확도를 더 효과적으로 감소
  • 이는 Motivation에서 예측한 대로 선형화된 모델이 더 나은 Weight Disentanglement를 달성하여 태스크 간 독립성이 향상됨을 보여줌
• 사전 학습의 중요성 증명
  • 무작위 초기화된 ViT에서는 Task Arithmetic이 작동하지 않음
  • 이는 Motivation에서 설명한 국소화된 Eigenfunction이 사전 학습을 통해 형성된다는 이론과 일치
  • Weight Disentanglement가 사전 학습의 창발적 특성임을 증명